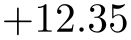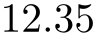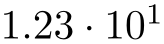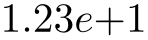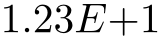TikZ and PGF Manual
Mathematical and Object-Oriented Engines
97 Number Printing¶
An extension by Christian Feuersänger
pgf supports number printing in different styles and rounds to arbitrary precision.
-
\pgfmathprintnumber{⟨x⟩} ¶
Generates pretty-printed output for the (real) number ⟨x⟩. The input number ⟨x⟩ is parsed using \pgfmathfloatparsenumber which allows arbitrary precision.
Numbers are typeset in math mode using the current set of number printing options, see below. Optional arguments can also be provided using \pgfmathprintnumber[⟨options⟩]⟨x⟩.
-
\pgfmathprintnumberto{⟨x⟩}{⟨macro⟩} ¶
Returns the resulting number into ⟨macro⟩ instead of typesetting it directly.
-
/pgf/number format/fixed(no value) ¶
Configures \pgfmathprintnumber to round the number to a fixed number of digits after the period, discarding any trailing zeros.
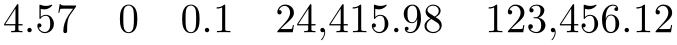
\pgfkeys{/pgf/number format/.cd,fixed,precision=2}
\pgfmathprintnumber{4.568}\hspace{1em}
\pgfmathprintnumber{5e-04}\hspace{1em}
\pgfmathprintnumber{0.1}\hspace{1em}
\pgfmathprintnumber{24415.98123}\hspace{1em}
\pgfmathprintnumber{123456.12345}
See section 97.1 for how to change the appearance.
-
/pgf/number format/fixed zerofill={⟨boolean⟩} (default true) ¶
Enables or disables zero filling for any number drawn in fixed point format.
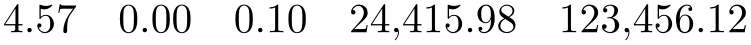
\pgfkeys{/pgf/number format/.cd,fixed,fixed zerofill,precision=2}
\pgfmathprintnumber{4.568}\hspace{1em}
\pgfmathprintnumber{5e-04}\hspace{1em}
\pgfmathprintnumber{0.1}\hspace{1em}
\pgfmathprintnumber{24415.98123}\hspace{1em}
\pgfmathprintnumber{123456.12345}
This key affects numbers drawn with fixed or std styles (the latter only if no scientific format is chosen).

\pgfkeys{/pgf/number format/.cd,std,fixed zerofill,precision=2}
\pgfmathprintnumber{4.568}\hspace{1em}
\pgfmathprintnumber{5e-05}\hspace{1em}
\pgfmathprintnumber{1}\hspace{1em}
\pgfmathprintnumber{123456.12345}
See section 97.1 for how to change the appearance.
-
/pgf/number format/sci(no value) ¶
Configures \pgfmathprintnumber to display numbers in scientific format, that means sign, mantissa and exponent (basis \(10\)). The mantissa is rounded to the desired precision (or sci precision, see below).

\pgfkeys{/pgf/number format/.cd,sci,precision=2}
\pgfmathprintnumber{4.568}\hspace{1em}
\pgfmathprintnumber{5e-04}\hspace{1em}
\pgfmathprintnumber{0.1}\hspace{1em}
\pgfmathprintnumber{24415.98123}\hspace{1em}
\pgfmathprintnumber{123456.12345}
See section 97.1 for how to change the exponential display style.
-
/pgf/number format/sci zerofill={⟨boolean⟩} (default true) ¶
Enables or disables zero filling for any number drawn in scientific format.

\pgfkeys{/pgf/number format/.cd,sci,sci zerofill,precision=2}
\pgfmathprintnumber{4.568}\hspace{1em}
\pgfmathprintnumber{5e-04}\hspace{1em}
\pgfmathprintnumber{0.1}\hspace{1em}
\pgfmathprintnumber{24415.98123}\hspace{1em}
\pgfmathprintnumber{123456.12345}
As with fixed zerofill, this option does only affect numbers drawn in sci format (or std if the scientific format is chosen).
See section 97.1 for how to change the exponential display style.
-
/pgf/number format/zerofill={⟨boolean⟩} (style, default true) ¶
Sets both fixed zerofill and sci zerofill at once.
-
/pgf/number format/std(no value) ¶
-
/pgf/number format/std=⟨lower e⟩(no default)
-
/pgf/number format/std=⟨lower e⟩:⟨upper e⟩(no default)
Configures \pgfmathprintnumber to a standard algorithm. It chooses either fixed or sci, depending on the order of magnitude. Let \(n=s \cdot m \cdot 10^e\) be the input number and \(p\) the current precision. If \(-p/2 \le e \le 4\), the number is displayed using fixed format. Otherwise, it is displayed using sci format.

\pgfkeys{/pgf/number format/.cd,std,precision=2}
\pgfmathprintnumber{4.568}\hspace{1em}
\pgfmathprintnumber{5e-04}\hspace{1em}
\pgfmathprintnumber{0.1}\hspace{1em}
\pgfmathprintnumber{24415.98123}\hspace{1em}
\pgfmathprintnumber{123456.12345}
The parameters can be customized using the optional integer argument(s): if \(\text {\meta {lower e}} \le e \le \text {\meta {upper e}}\), the number is displayed in fixed format, otherwise in sci format. Note that ⟨lower e⟩ should be negative for useful results. The precision used for the scientific format can be adjusted with sci precision if necessary.
-
/pgf/number format/relative*=⟨exponent base 10⟩(no default) ¶
Configures \pgfmathprintnumber to format numbers relative to an order of magnitude, \(10^r\), where \(r\) is an integer number.
This key addresses different use-cases.
provide a unified format for a sequence of numbers. Consider the following test:

\pgfkeys{/pgf/number format/relative*={1}}
\pgfmathprintnumber{6.42e-16}\hspace{1em}
\pgfmathprintnumber{1.2}\hspace{1em}
\pgfmathprintnumber{6}\hspace{1em}
\pgfmathprintnumber{20.6}\hspace{1em}
\pgfmathprintnumber{87}
With any other style, the 6.42e-16 would have been formatted as an isolated number. Here, it is rounded to 0 because when viewed relative to \(10^1\) (the exponent \(1\) is the argument for relative), it has no significant digits.

\pgfkeys{/pgf/number format/relative*={2}}
\pgfmathprintnumber{123.345}\hspace{1em}
\pgfmathprintnumber{0.0012}\hspace{1em}
\pgfmathprintnumber{0.0014}\hspace{1em}
The example above applies the initial precision=2 to 123.345 – relative to \(100\). Two significant digits of 123.345 relative to \(100\) are 123. Note that the “\(2\) significant digits of 123.345” translates to “round 1.2345 to \(2\) digits”, which would yield 1.2300. Similarly, the other two numbers are 0 compared to \(100\) using the given precision.

\pgfkeys{/pgf/number format/relative*={-3}}
\pgfmathprintnumber{123.345}\hspace{1em}
\pgfmathprintnumber{0.0012}\hspace{1em}
\pgfmathprintnumber{0.0014}\hspace{1em}
improve rounding in the presence of inaccurate numbers. Let us suppose that some limited-precision arithmetic resulted in the result 123456999 (like the fpu of pgf). You know that its precision is about five or six significant digits. And you want to provide a fixed point output. In this case, the trailing digits ....999 are a numerical artifact due to the limited precision. Use relative*=3,precision=0 to eliminate the artifacts:

\pgfkeys{/pgf/number format/.cd,relative*={3},precision=0}
\pgfmathprintnumber{123456999}\hspace{1em}
\pgfmathprintnumber{123456999.12}
Here, precision=0 means that we inspect 123456.999 and round that number to \(0\) digits. Finally, we move the period back to its initial position. Adding relative style=fixed results in fixed point output format:

\pgfkeys{/pgf/number format/.cd,relative*={3},precision=0,relative style=fixed}
\pgfmathprintnumber{123456999}\hspace{1em}
\pgfmathprintnumber{123456999.12}
Note that there is another alternative for this use-case which is discussed later: the fixed relative style.

\pgfkeys{/pgf/number format/.cd,fixed relative,precision=6}
\pgfmathprintnumber{123456999}\hspace{1em}
\pgfmathprintnumber{123456999.12}
You might wonder why there is an asterisk in the key’s name. The short answer is: there is also a /pgf/number format/relative number printer which does unexpected things. The key relative* repairs this. Existing code will still use the old behavior.
Technically, the key works as follows: as already explained above, relative*=3 key applied to 123456999.12 moves the period by three positions and analyzes 123456.99912. Mathematically speaking, we are given a number \(x = \pm m \cdot 10^e\) and we attempt to apply relative*=\(r\). The method then rounds \(x / 10^r\) to precision digits. Afterwards, it multiplies the result by \(10^r\) and typesets it.
-
/pgf/number format/every relative(style, no value) ¶
A style which configures how the relative method finally displays its results.
The initial configuration is
Note that rounding is turned off when the resulting style is being evaluated (since relative already rounded the number).
Although supported, I discourage from using fixed zerofill or sci zerofill in this context – it may lead to a suggestion of higher precision than is actually used (because fixed zerofill might simply add .00 although there was a different information before relative rounded the result).
-
/pgf/number format/relative style={⟨options⟩}(no default) ¶
The same as every relative/.append style={⟨options⟩}.
-
/pgf/number format/fixed relative(no value) ¶
Configures \pgfmathprintnumber to format numbers in a similar way to the fixed style, but the precision is interpreted relatively to the number’s exponent.
The motivation is to get the same rounding effect as for sci, but to display the number in the fixed style:

\pgfkeys{/pgf/number format/.cd,fixed relative,precision=3}
\pgfmathprintnumber{1000.0123}\hspace{1em}
\pgfmathprintnumber{100.0567}\hspace{1em}
\pgfmathprintnumber{0.000010003452}\hspace{1em}
\pgfmathprintnumber{0.010073452}\hspace{1em}
\pgfmathprintnumber{1.23567}\hspace{1em}
\pgfmathprintnumber{1003.75}\hspace{1em}
\pgfmathprintnumber{1006.75}\hspace{1em}
The effect of fixed relative is that the number is rounded to exactly the first ⟨precision⟩ non-zero digits, no matter how many leading zeros the number might have.
Use fixed relative if you want fixed and if you know that only the first \(n\) digits are correct. Use sci if you need a scientific display style and only the first \(n\) digits are correct.
Note that fixed relative ignores the fixed zerofill flag.
See also the relative* key. Note that the relative={⟨exponent⟩} key explicitly moves the period to some designated position before it attempts to round the number. Afterwards, it “rounds from the right”, i.e. it rounds to that explicitly chosen digit position. In contrast to that, fixed relative “rounds from the left”: it takes the first non-zero digit, temporarily places the period after this digit, and rounds that number. The rounding style fixed leaves the period where it is, and rounds everything behind that digit. The sci style is similar to fixed relative.
-
/pgf/number format/int detect(no value) ¶
Configures \pgfmathprintnumber to detect integers automatically. If the input number is an integer, no period is displayed at all. If not, the scientific format is chosen.

\pgfkeys{/pgf/number format/.cd,int detect,precision=2}
\pgfmathprintnumber{15}\hspace{1em}
\pgfmathprintnumber{20}\hspace{1em}
\pgfmathprintnumber{20.4}\hspace{1em}
\pgfmathprintnumber{0.01}\hspace{1em}
\pgfmathprintnumber{0}
-
\pgfmathifisint{⟨number constant⟩}{⟨true code⟩}{⟨false code⟩} ¶
A command which does the same check as int detect, but it invokes ⟨true code⟩ if the ⟨number constant⟩ actually is an integer and the ⟨false code⟩ if not.
As a side-effect, \pgfretval will contain the parsed number, either in integer format or as parsed floating point number.
The argument ⟨number constant⟩ will be parsed with \pgfmathfloatparsenumber.

15
\pgfmathifisint{15}{is
an int:
\pgfretval.}{is
no int}\hspace{1em}
15.5
\pgfmathifisint{15.5}{is an
int:
\pgfretval.}{is
no
int}
-
/pgf/number format/int trunc(no value) ¶
Truncates every number to integers (discards any digit after the period).
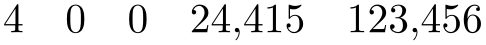
\pgfkeys{/pgf/number format/.cd,int trunc}
\pgfmathprintnumber{4.568}\hspace{1em}
\pgfmathprintnumber{5e-04}\hspace{1em}
\pgfmathprintnumber{0.1}\hspace{1em}
\pgfmathprintnumber{24415.98123}\hspace{1em}
\pgfmathprintnumber{123456.12345}
-
/pgf/number format/frac(no value) ¶
-
/pgf/number format/frac TeX={⟨\macro⟩} (no default, initially \frac) ¶
-
/pgf/number format/frac denom=⟨int⟩ (no default, initially empty) ¶
-
/pgf/number format/frac whole=true|false (no default, initially true) ¶
-
/pgf/number format/frac shift={⟨integer⟩} (no default, initially 4) ¶
Displays numbers as fractionals.
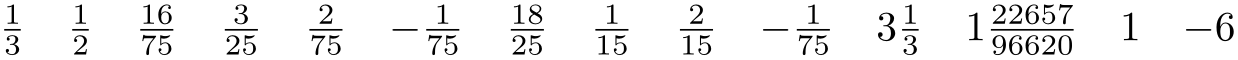
\usetikzlibrary {fpu}
\pgfkeys{/pgf/number format/frac}
\pgfmathprintnumber{0.333333333333333}\hspace{1em}
\pgfmathprintnumber{0.5}\hspace{1em}
\pgfmathprintnumber{2.133333333333325e-01}\hspace{1em}
\pgfmathprintnumber{0.12}\hspace{1em}
\pgfmathprintnumber{2.666666666666646e-02}\hspace{1em}
\pgfmathprintnumber{-1.333333333333334e-02}\hspace{1em}
\pgfmathprintnumber{7.200000000000000e-01}\hspace{1em}
\pgfmathprintnumber{6.666666666666667e-02}\hspace{1em}
\pgfmathprintnumber{1.333333333333333e-01}\hspace{1em}
\pgfmathprintnumber{-1.333333333333333e-02}\hspace{1em}
\pgfmathprintnumber{3.3333333}\hspace{1em}
\pgfmathprintnumber{1.2345}\hspace{1em}
\pgfmathprintnumber{1}\hspace{1em}
\pgfmathprintnumber{-6}
Allows to use a different implementation for \frac inside of the frac display type.
Allows to provide a custom denominator for frac.
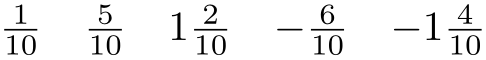
\usetikzlibrary {fpu}
\pgfkeys{/pgf/number format/.cd,frac, frac denom=10}
\pgfmathprintnumber{0.1}\hspace{1em}
\pgfmathprintnumber{0.5}\hspace{1em}
\pgfmathprintnumber{1.2}\hspace{1em}
\pgfmathprintnumber{-0.6}\hspace{1em}
\pgfmathprintnumber{-1.4}\hspace{1em}
Configures whether complete integer parts shall be placed in front of the fractional part. In this case, the fractional part will be less then \(1\). Use frac whole=false to avoid whole number parts.
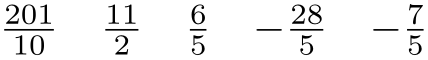
\usetikzlibrary {fpu}
\pgfkeys{/pgf/number format/.cd,frac, frac whole=false}
\pgfmathprintnumber{20.1}\hspace{1em}
\pgfmathprintnumber{5.5}\hspace{1em}
\pgfmathprintnumber{1.2}\hspace{1em}
\pgfmathprintnumber{-5.6}\hspace{1em}
\pgfmathprintnumber{-1.4}\hspace{1em}
In case you experience problems because of stability problems, try experimenting with a different frac shift. Higher shift values \(k\) yield higher sensitivity to inaccurate data or inaccurate arithmetic.
Technically, the following happens. If \(r < 1\) is the fractional part of the mantissa, then a scale \(i = 1/r \cdot 10^k\) is computed where \(k\) is the shift; fractional parts of \(i\) are neglected. The value \(1/r\) is computed internally, its error is amplified.
If you still experience stability problems, use \usepackage{fp} in your preamble. The frac style will then automatically employ the higher absolute precision of fp for the computation of \(1/r\).
-
/pgf/number format/precision={⟨number⟩}(no default) ¶
Sets the desired rounding precision for any display operation. For scientific format, this affects the mantissa.
-
/pgf/number format/sci precision=⟨number or empty⟩ (no default, initially empty) ¶
Sets the desired rounding precision only for sci styles.
Use sci precision={} to restore the initial configuration (which uses the argument provided to precision for all number styles).
-
/pgf/number format/read comma as period=true|false (no default, initially false) ¶
This is one of the few keys which allows to customize the number parser. If this switch is turned on, a comma is read just as a period.
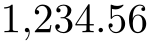
This is typically undesired as it can cause side-effects with math parsing instructions. However, it is supported to format input numbers or input tables. Consider use comma to typeset the result with a comma as well.
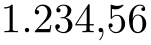
\pgfkeys{/pgf/number format/.cd,
read comma as period,
use comma}
\pgfmathprintnumber{1234,56}
97.1 Changing display styles¶
You can change the way how numbers are displayed. For example, if you use the ‘fixed’ style, the input number is rounded to the desired precision and the current fixed point display style is used to typeset the number. The same is applied to any other format: first, rounding routines are used to get the correct digits, afterwards a display style generates proper TeX-code.
-
/pgf/number format/set decimal separator={⟨text⟩}(no default) ¶
Assigns {⟨text⟩} as decimal separator for any fixed point numbers (including the mantissa in sci format).
Use \pgfkeysgetvalue{/pgf/number format/set decimal separator}\value to get the current separator into \value.
-
/pgf/number format/dec sep={⟨text⟩}(style, no default) ¶
Just another name for set decimal separator.
-
/pgf/number format/set thousands separator={⟨text⟩}(no default) ¶
Assigns {⟨text⟩} as thousands separator for any fixed point numbers (including the mantissa in sci format).
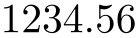
\pgfkeys{/pgf/number format/.cd,
fixed,
fixed zerofill,
precision=2,
set thousands separator={}}
\pgfmathprintnumber{1234.56}

\pgfkeys{/pgf/number format/.cd,
fixed,
fixed zerofill,
precision=2,
set thousands separator={}}
\pgfmathprintnumber{1234567890}

\pgfkeys{/pgf/number format/.cd,
fixed,
fixed zerofill,
precision=2,
set thousands separator={.}}
\pgfmathprintnumber{1234567890}

\pgfkeys{/pgf/number format/.cd,
fixed,
fixed zerofill,
precision=2,
set thousands separator={,}}
\pgfmathprintnumber{1234567890}
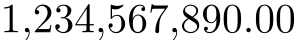
\pgfkeys{/pgf/number format/.cd,
fixed,
fixed zerofill,
precision=2,
set thousands separator={{{,}}}}
\pgfmathprintnumber{1234567890}
The last example employs commas and disables the default comma-spacing.
Use \pgfkeysgetvalue{/pgf/number format/set thousands separator}\value to get the current separator into \value.
-
/pgf/number format/1000 sep={⟨text⟩}(style, no default) ¶
Just another name for set thousands separator.
-
/pgf/number format/1000 sep in fractionals={⟨boolean⟩} (no default, initially false) ¶
Configures whether the fractional part should also be grouped into groups of three digits.
The value true will active the 1000 sep for both, integer and fractional parts. The value false will active 1000 sep only for the integer part.
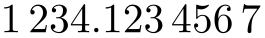
\pgfkeys{/pgf/number format/.cd,
fixed,
precision=999,
set thousands separator={\,},
1000 sep in fractionals,
}
\pgfmathprintnumber{1234.1234567}
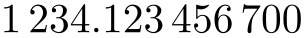
\pgfkeys{/pgf/number format/.cd,
fixed,fixed zerofill,
precision=9,
set thousands separator={\,},
1000 sep in fractionals,
}
\pgfmathprintnumber{1234.1234567}
Testing comma to see what happens after the end of key.
-
/pgf/number format/min exponent for 1000 sep={⟨number⟩} (no default, initially 0) ¶
Defines the smallest exponent in scientific notation which is required to draw thousand separators. The exponent is the number of digits minus one, so \(\meta {number}=4\) will use thousand separators starting with \(1e4 = 10000\).
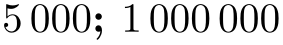
\pgfkeys{/pgf/number format/.cd,
int detect,
1000 sep={\,},
min exponent for 1000 sep=0}
\pgfmathprintnumber{5000}; \pgfmathprintnumber{1000000}

\pgfkeys{/pgf/number format/.cd,
int detect,
1000 sep={\,},
min exponent for 1000 sep=4}
\pgfmathprintnumber{1000}; \pgfmathprintnumber{5000}
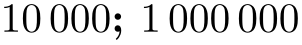
\pgfkeys{/pgf/number format/.cd,
int detect,
1000 sep={\,},
min exponent for 1000 sep=4}
\pgfmathprintnumber{10000}; \pgfmathprintnumber{1000000}
A value of 0 disables this feature (negative values are ignored).
Checking comma.
-
/pgf/number format/use period(no value) ¶
A predefined style which installs periods “.” as decimal separators and commas “,” as thousands separators. This style is the default.
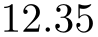
\pgfkeys{/pgf/number format/.cd,fixed,precision=2,use period}
\pgfmathprintnumber{12.3456}
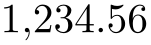
\pgfkeys{/pgf/number format/.cd,fixed,precision=2,use period}
\pgfmathprintnumber{1234.56}
-
/pgf/number format/use comma(no value) ¶
A predefined style which installs commas “,” as decimal separators and periods “.” as thousands separators.
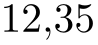
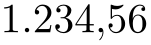
-
/pgf/number format/skip 0.={⟨boolean⟩} (no default, initially false) ¶
Configures whether numbers like \(0.1\) shall be typeset as \(.1\) or not.
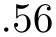
\pgfkeys{/pgf/number format/.cd,
fixed,
fixed zerofill,precision=2,
skip 0.}
\pgfmathprintnumber{0.56}
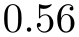
\pgfkeys{/pgf/number format/.cd,
fixed,
fixed zerofill,precision=2,
skip 0.=false}
\pgfmathprintnumber{0.56}
-
/pgf/number format/print sign={⟨boolean⟩}(style, no default) ¶
A style which is simply an alias for showpos={⟨boolean⟩}.
-
/pgf/number format/sci 10^e(no value) ¶
The same as ‘sci 10e’.
-
/pgf/number format/sci subscript(no value) ¶
Typesets the exponent as subscript for any number displayed in scientific format. This style requires very little space.

\pgfkeys{/pgf/number format/.cd,sci,sci subscript}
\pgfmathprintnumber{12.345}
-
/pgf/number format/sci superscript(no value) ¶
Typesets the exponent as superscript for any number displayed in scientific format. This style requires very little space.
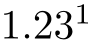
\pgfkeys{/pgf/number format/.cd,sci,sci superscript}
\pgfmathprintnumber{12.345}
-
/pgf/number format/sci generic={⟨keys⟩}(no default) ¶
-
/pgf/number format/sci generic/mantissa sep={⟨text⟩} (no default, initially empty) ¶
-
/pgf/number format/sci generic/exponent={⟨text⟩} (no default, initially empty) ¶
Allows to define an own number style for the scientific format. Here, ⟨keys⟩ can be one of the following choices (omit the long key prefix):
Provides the separator between a mantissa and the exponent. It might be \cdot, for example,
Provides text to format the exponent. The actual exponent is available as argument #1 (see below).
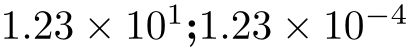
\pgfkeys{
/pgf/number format/.cd,
sci,
sci generic={mantissa sep=\times,exponent={10^{#1}}}}
\pgfmathprintnumber{12.345};
\pgfmathprintnumber{0.00012345}
The ⟨keys⟩ can depend on three parameters, namely on #1 which is the exponent, #2 containing the flags entity of the floating point number and #3 is the (unprocessed and unformatted) mantissa.
Note that sci generic is not suitable to modify the appearance of fixed point numbers, nor can it be used to format the mantissa (which is typeset like fixed point numbers). Use dec sep, 1000 sep and print sign to customize the mantissa.
-
/pgf/number format/retain unit mantissa=true|false (no default, initially true) ¶
Allows to omit a unit mantissa.
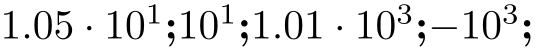
\pgfkeys{
/pgf/number format/.cd,
sci, retain unit mantissa=false}
\pgfmathprintnumber{10.5};
\pgfmathprintnumber{10};
\pgfmathprintnumber{1010};
\pgfmathprintnumber[precision=1]{-1010};
The feature is applied after rounding to the desired precision: if the remaining mantissa is equal to \(1\), it will be omitted. It applies to all styles involving the scientific format (including std).
-
/pgf/number format/@dec sep mark={⟨text⟩}(no default) ¶
Will be placed right before the place where a decimal separator belongs to. However, {⟨text⟩} will be inserted even if there is no decimal separator. It is intended as place-holder for auxiliary routines to find alignment positions.
This key should never be used to change the decimal separator! Use dec sep instead.
-
/pgf/number format/@sci exponent mark={⟨text⟩}(no default) ¶
Will be placed right before exponents in scientific notation. It is intended as place-holder for auxiliary routines to find alignment positions.
This key should never be used to change the exponent!
-
/pgf/number format/assume math mode={⟨boolean⟩} (default true) ¶
Set this to true if you don’t want any checks for math mode. The initial setting checks whether math mode is active using \pgfutilensuremath for each final number.
Use assume math mode=true if you know that math mode is active. In that case, the final number is typeset as-is, no further checking is performed.
-
/pgf/number format/verbatim(style, no value) ¶
A style which configures the number printer to produce verbatim text output, i.e., it doesn’t contain TeX macros.

\usetikzlibrary {fpu}
\pgfkeys{
/pgf/fpu,
/pgf/number format/.cd,
sci,
verbatim}
\pgfmathprintnumber{12.345};
\pgfmathprintnumber{0.00012345};
\pgfmathparse{exp(15)}
\pgfmathprintnumber{\pgfmathresult}
The style resets 1000 sep, dec sep, print sign, skip 0. and sets assume math mode. Furthermore, it installs a sci generic format for verbatim output of scientific numbers.
However, it will still respect precision, fixed zerofill, sci zerofill and the overall styles fixed, sci, int detect (and their variants). It might be useful if you intend to write output files.