Manual for Package pgfplots
2D/3D Plots in LATeX, Version 1.18.2
https://github.com/pgf-tikz/pgfplots
Utilities and Basic Level Commands
9.1Utility Commands
-
\foreach
variables
in
list
{commands}
A powerful loop command provided by TikZ, see the TikZ manual for details.
Iterating 1. Iterating 2. Iterating 3. Iterating 4.
\foreach \x in {1,2,...,4} {Iterating
\x. }%
A pgfplots related example could be
-
\pgfplotsforeachungrouped
variable
in
list
{command}
A specialised variant of \foreach which can do
two things: it does not introduce extra groups while executing
command
and it allows to invoke the math parser for (simple!)
\(x_0\),\(x_1\),...,\(x_n\)
expressions.
Iterating 1. Iterating 2. Iterating 3. Iterating 4. All collected = , 1, 2, 3, 4.
\def\allcollected{}
\pgfplotsforeachungrouped \x in {1,2,...,4} {Iterating \x. \edef\allcollected{\allcollected, \x}}%
All collected = \allcollected.
A more useful example might be to work with tables. The following example is taken from PgfplotsTable:
\pgfplotsforeachungrouped \i in {1,2,...,10} {%
\pgfplotstablevertcat{\output}{datafile\i} % appends `datafile\i' -> `\output'
}%
% since it was ungrouped, \output is still defined (would not work
% with \foreach)
The special syntax
list=\(x_0\),\(x_1\),...,\(x_n\), i.e. with two leading elements, followed by dots and a final element, invokes the math parser for the loop. Thus, it allows
larger number ranges than any other syntax if /pgf/fpu is
active. In all other cases,
\pgfplotsforeachungrouped invokes
\foreach and provides the results without
TeX
groups.
Keep in mind that inside of an axis environment, all loop constructions (including custom loops, \foreach and \pgfplotsforeachungrouped) need to be handled with care: loop arguments can only be used in places where they are immediately evaluated; but pgfplots postpones the evaluation of many macros. For example, to loop over something and to generate axis descriptions of the form \node at (axis cs:\i,0.5)..., the loop macro \i will be evaluated in \end{axis} – but at that time, the loop is over and its value is lost. The correct way to handle such an application is to expand the loop variable explicitly. For example:
\pgfplotsforeachungrouped \i/\j in {
1 / a,
2 / b,
3 / c
}{
\edef\temp{\noexpand\node at (axis cs: \i,0.5) {\j};}
% \show\temp % lets TeX show you what \temp contains
\temp
}
The example generates three loop iterations: \i=1, \j=a; then \i=2, j=b; then \i=3, \j=c. Inside of the loop body, it expands them and assigns the result to a macro using an “expanded definition”, \edef. The result no longer contains either \i or \j (since these have been expanded). Then, it invokes the resulting macro. Details about the TeX command \edef and expansion control can be found in the document TeX-programming-notes.pdf which comes with pgfplots.
-
\pgfplotsinvokeforeach{
list} {command}
A variant of
\pgfplotsforeachungrouped (and
such also of \foreach) which replaces any occurrence of #1 inside of
command
once for every element in
list. Thus, it actually assumes that {command} is like a \newcommand body.
In other words,
command
is invoked for every element of
list. The actual element of
list
is available as #1.
As \pgfplotsforeachungrouped, this command does not introduce extra scopes (i.e. it is ungrouped as well).
The difference to \foreach \x in list{command} is subtle: the \x would not be expanded whereas #1 is.
Invoke them: [a] [b] [c] [d]
The counter example would use a macro (here \x) as loop argument:
Invoke them: [d] [d] [d] [d]
you can’t nest this command yet (since it does not introduce protection by scopes).
-
\pgfmathparse{
expression}
¶
Invokes the pgf math parser for
expression
and defines \pgfmathresult to be the result.
The result is ‘42.0’.
The math engine in pgf typically uses TeX’s internal arithmetics. That means: it is well suited for numbers in the range \([-16384,16384]\) and has a precision of \(5\) digits.
The number range is typically too small for plotting applications. pgfplots improves the number range by means of \pgfkeys{/pgf/fpu}\pgfmathparse{1+41} to activate the “floating point unit” (fpu) and to apply all following operations in floating point.
In pgfplots, the key /pgfplots/use fpu is typically on, which means that any coordinate arithmetics are carried out with the fpu. However, all pgf related drawing operations still use the standard math engine.
In case you ever need to process numbers of extended precision, you may want to use
The result is ‘1 · 106 ’.
Note that results of the fpu are typically not in human-readable format, so \pgfmathprintnumber is the preferred way to typeset such numbers.
Please refer to the PGF/TikZ manual for more details.
-
/pgfplots/use fpu=true|false (initially true) ¶
pgfplots comes with different approaches to compute math expressions and use fpu is the most powerful. It implements math operations either in the lua backend or in a pure TeX implementation and comes with a high number range and adequate precision.
However, the values stored in \pgfmathresult are cryptic and need to be processed by means of special macros. The switch use fpu is only useful if this number format results in difficulties, i.e. it is a debug switch which should never be used in normal operations.
-
/pgf/declare function=
function definitions
¶
Allows to define one or more functions.
The argument
function definitions
can contain one or more definitions, and each must be terminated by a semicolon:
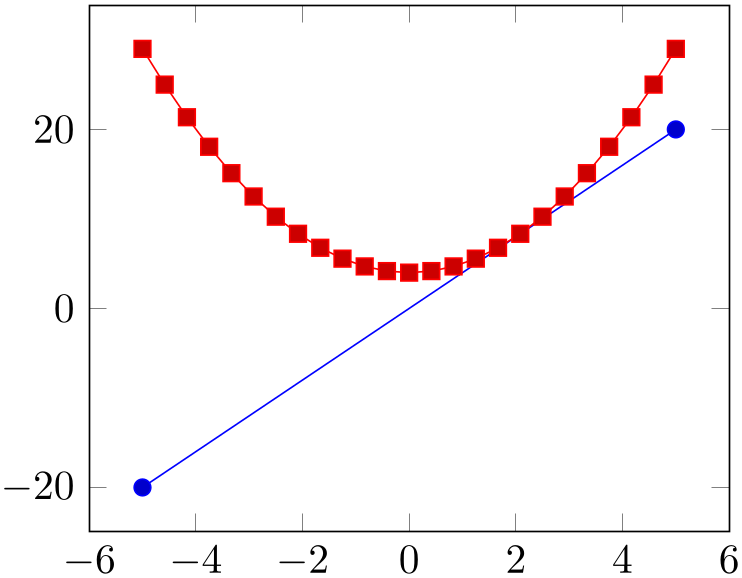
% Preamble: \pgfplotsset{width=7cm,compat=1.18}
\begin{tikzpicture}
\begin{axis}[
declare function={
C=4;
square(\t)=(\t)^2 + C;
},
]
\addplot+ [samples=2] {C*x};
\addplot {square(x)};
\end{axis}
\end{tikzpicture}
The definitions as such have the form
functionargument list
=
definition
where the
argument list
contains a comma-separated-list of arguments like \t or \t,\a,\b. The
definition
is a math expression which makes use of these arguments.
Please refer to the PGF/TikZ manual for more details.
-
\pgfplotsiffileexists{
filename}{true code}{false code}
¶
Invokes
true code
if
filename
exists and
false code
if not. Can be used in looping macros, for example to plot every data file until there are no more of them.
-
\pgfplotsutilifstringequal{
first}{second}{true code}{false code}
¶
A simple “strcmp” tool which invokes
true code
if
first
\(=\)second
and
false code
otherwise. This does not expand macros.
-
\pgfkeys ¶
-
\pgfeov ¶
-
\pgfkeysvalueof ¶
-
\pgfkeysgetvalue ¶
These commands are part of the TikZ way of specifying options, its sub-package pgfkeys. The \pgfplotsset command is actually nothing but a wrapper around \pgfkeys.
A short introduction into \pgfkeys can be found in [9] whereas the complete reference is, of course, the PGF/TikZ manual.
The key \pgfkeysvalueof{key name} expands to the value of a key; \pgfkeysgetvalue{key name}{\macro} stores the value of
key name
into
\macro. The \pgfeov macro is used to delimit arguments for code
keys in \pgfkeys, please refer to the references mentioned above.